Понимание базиса является важным аспектом в линейной алгебре и математическом анализе. При работе с векторами необходимо определить, могут ли они быть использованы в качестве базисных. Базис - это набор векторов, которые образуют линейно независимую систему и могут быть использованы для представления любого вектора в данном пространстве. Определение возможности принятия векторов за базисные требует проведения нескольких шагов и анализа свойств векторов.
Первый шаг в определении возможности принятия векторов за базисные - проверка линейной независимости. Для этого необходимо установить, что никакая из векторов не может быть выражена в виде линейной комбинации других векторов. Если это условие выполняется, то векторы являются линейно независимыми и потенциально могут быть использованы в качестве базисных.
Второй шаг - проверка спана. Чтобы векторы могли служить базисом, они должны охватывать всё пространство. Другими словами, векторы должны образовывать систему, способную представить любой другой вектор в этом пространстве. Если векторы охватывают всё пространство, то они могут быть приняты за базисные.
Наконец, третий шаг - проверка размерности. Размерность - это количество базисных векторов, необходимых для представления пространства. Чтобы векторы могли быть базисными, их количество должно соответствовать размерности пространства. Если количество векторов равно размерности, то векторы могут быть приняты за базисные.
Все эти шаги позволяют определить, могут ли векторы быть использованы в качестве базисных. Правильное определение базиса помогает решать различные задачи в линейной алгебре, включая решение систем линейных уравнений и линейное преобразование. Поэтому понимание и умение определять возможность принятия векторов за базисные является важным навыком в математике.
Определение базисных векторов
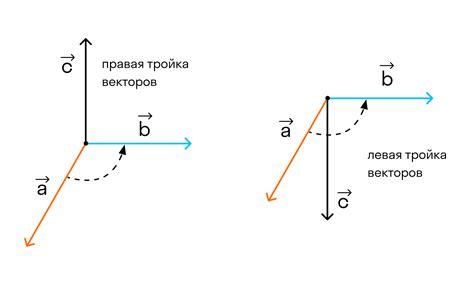
Для определения базисных векторов необходимо проверить два условия:
- Линейная независимость: векторы должны быть линейно независимыми, то есть ни один вектор не может быть представлен в виде линейной комбинации других векторов.
- Охватывающий набор: векторы должны способны породить все возможные векторы в данном линейном пространстве. Другими словами, каждый вектор должен быть линейной комбинацией базисных векторов.
Чтобы проверить линейную независимость векторов, можно составить матрицу из данных векторов, и применить к ней метод Гаусса. Если после приведения матрицы к ступенчатому виду получается нулевая строка, значит векторы линейно зависимы и не могут быть базисными.
Охватывающий набор базисных векторов можно проверить, умножив каждый вектор на матрицу коэффициентов и сравнить результаты с соответствующими векторами. Если все векторы возможно представить как линейную комбинации базисных векторов, то они являются базисными.
Определение базисных векторов является важным шагом при работе с преобразованием и анализом векторов в различных областях, таких как алгебра, физика, и компьютерная графика.
| Пример: | Определение базисных векторов в трехмерном пространстве |
|---|---|
| Вектор 1: | [1, 0, 0] |
| Вектор 2: | [0, 1, 0] |
| Вектор 3: | [0, 0, 1] |
В данном примере, векторы [1, 0, 0], [0, 1, 0], и [0, 0, 1] являются базисными векторами, так как они линейно независимы и способны породить любой вектор в трехмерном пространстве.
Ограничения для базисных векторов

Векторы, которые можно выбрать в качестве базисных, должны удовлетворять определенным ограничениям. Это необходимо для того, чтобы базисные векторы могли полностью описывать пространство, которое они порождают.
Основные ограничения для базисных векторов:
- Линейная независимость:
Базисные векторы должны быть линейно независимыми, то есть ни один из них не может быть выражен через комбинацию других векторов. Если один из векторов является линейной комбинацией других векторов, то он не может быть выбран в качестве базисного. - Порождаемость пространства:
Базисные векторы должны порождать всё пространство. Это означает, что любой вектор в пространстве должен быть представим в виде линейной комбинации базисных векторов. Если какой-то вектор не может быть представлен таким образом, то базисные векторы этим условием не удовлетворяют. - Максимальность:
Базис должен быть максимальным, то есть нельзя добавить ни один вектор, не нарушив первые два условия, чтобы все три условия выполнялись одновременно. Это означает, что базис должен содержать наименьшее возможное количество векторов.
Соблюдение всех этих ограничений гарантирует, что базисные векторы предоставляют полную информацию о пространстве и могут быть использованы для описания и выполнения операций над векторами.
Критерии выбора базисных векторов

При выборе базисных векторов важно учитывать несколько критериев:
- Линейная независимость: базисные векторы должны быть линейно независимыми, то есть ни один из них не может быть линейной комбинацией других. Это гарантирует, что каждый вектор в пространстве может быть выражен уникальным образом через базисные векторы.
- Охватывающость: базисные векторы должны охватывать всё пространство. Это значит, что любой вектор в пространстве должен быть линейной комбинацией базисных векторов.
- Минимальность: базис должен содержать наименьшее количество векторов, при котором выполняются первые два условия. Минимальность базиса позволяет более компактно и удобно представлять вектора в пространстве.
Выбор базисных векторов играет важную роль в анализе и решении линейных систем уравнений, нахождении собственных значений и векторов, а также в других задачах, связанных с линейными пространствами.
Практические примеры определения базисных векторов
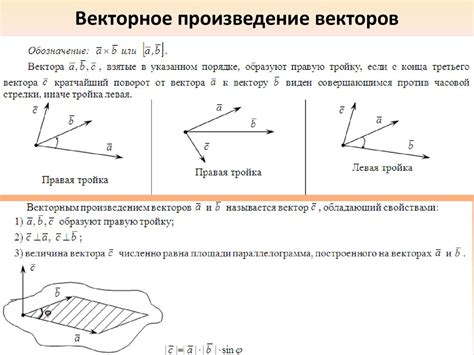
Практическим примером определения базисных векторов может служить пространство трехмерного векторного пространства. Здесь базисными векторами являются обычно единичные векторы, направленные вдоль координатных осей: i, j и k. Они образуют линейно независимую систему, то есть ни один из этих векторов не может быть представлен в виде линейной комбинации других двух.
Еще одним примером может служить базис векторного пространства, состоящего из полиномов степени не выше некоторого фиксированного числа n. В этом случае базисными векторами являются полиномы 1, x, x^2, ..., x^n. Каждый полином может быть выражен в виде линейной комбинации этой системы базисных векторов.
Определение базисных векторов может быть полезно в различных областях, например, в компьютерной графике для описания трехмерных объектов, в квантовой механике для описания состояний системы и так далее. Знание и использование базисных векторов помогает сократить количество информации и упростить анализ и решение задач.



