Базис в линейной алгебре играет очень важную роль. Он является основой для построения пространства, а его векторы позволяют описывать и выражать любой другой вектор в этом пространстве. Поэтому так важно уметь определить, являются ли заданные векторы базисом.
Главное условие для того, чтобы векторы являлись базисом - они должны быть линейно независимыми. Векторы линейно независимы, если ни один из них не может быть выражен через линейные комбинации остальных векторов с ненулевыми коэффициентами. Иными словами, если уравнение a1*v1 + a2*v2 + ... + an*vn = 0 имеет только тривиальное решение (все коэффициенты равны 0), то векторы образуют базис.
Для проверки, являются ли заданные векторы базисом, можно составить систему уравнений и решить ее. Если решение системы даёт только тривиальные коэффициенты, то векторы образуют базис. Если же существуют нетривиальные решения, то векторы линейно зависимы и не образуют базис.
Также можно воспользоваться определителем матрицы, составленной из векторов. Если определитель матрицы равен нулю, то векторы линейно зависимы и не образуют базис. Если определитель не равен нулю, то векторы линейно независимы и образуют базис.
Определение базиса векторов

Другими словами, для заданного векторного пространства, базис является минимальным набором векторов, который может порождать все остальные векторы из этого пространства.
Для определения базиса необходимо проверить два условия:
- Линейная независимость: Если ни один вектор из базиса не может быть выражен через линейную комбинацию остальных векторов базиса, то они являются линейно независимыми.
- Спан: Если любой вектор из векторного пространства может быть представлен как линейная комбинация векторов базиса, то эти векторы образуют спан пространства.
Если все векторы из пространства удовлетворяют этим двум условиям, то эти векторы образуют базис векторного пространства.
Количество векторов в базисе

Количество векторов в базисе задает размерность пространства, которое они порождают. То есть, если векторы образуют базис, то любой другой вектор может быть линейно выражен через них. Поэтому, количество векторов в базисе очень важно для определения размерности пространства.
Пусть у нас есть набор векторов V1, V2, ..., Vn. Чтобы эти векторы образовали базис, необходимо и достаточно, чтобы они были линейно независимы и линейно охватывали всё пространство.
| Условие | Количество векторов в базисе | Размерность пространства |
|---|---|---|
| Линейная независимость | n ≥ 1 | n-мерное пространство |
| Охватывание всего пространства | n ≤ размерность пространства | n-мерное пространство |
| Линейная независимость и охватывание всего пространства | n = размерность пространства | n-мерное пространство |
Если количество векторов в базисе не соответствует размерности пространства, то такие векторы называются пространственно не согласованными, и они не образуют базис.
Линейная независимость векторов в базисе

Для проверки линейной независимости векторов в базисе можно использовать определитель матрицы, составленной из этих векторов. Если определитель равен нулю, то векторы линейно зависимы и не могут образовывать базис.
Линейная независимость векторов в базисе играет важную роль в линейной алгебре и применяется во многих областях, включая физику, математику и компьютерные науки.
Координатная запись векторов в базисе
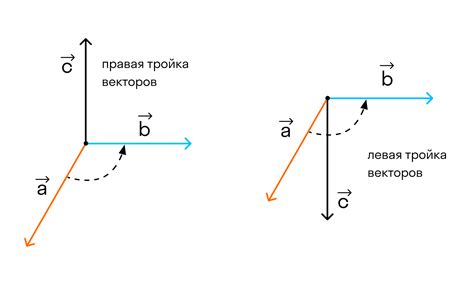
Для того чтобы записать вектор в координатной форме, необходимо задать базис пространства. Базис – это набор линейно независимых векторов, которые позволяют описать любой вектор пространства. Обычно базис состоит из перпендикулярных векторов. Примером базиса может служить ортонормированный базис, в котором все векторы имеют длину 1 и перпендикулярны друг другу.
Для записи вектора в координатной форме в базисе используются числа, которые называются координатами вектора. Координаты вектора соответствуют проекциям этого вектора на каждый вектор базиса. Например, если базис состоит из двух векторов a и b, то координаты вектора v в этом базисе будут представлены парой чисел (x, y), где x – проекция вектора v на вектор a, y – проекция вектора v на вектор b.
Координатная запись векторов в базисе позволяет выполнять различные операции над векторами, такие как сложение и умножение на число. Для сложения векторов в координатной форме достаточно сложить соответствующие координаты. Например, для двух векторов v1 = (x1, y1) и v2 = (x2, y2) их сумма будет равна v1 + v2 = (x1 + x2, y1 + y2).
Координатная запись векторов в базисе также позволяет выражать линейные комбинации векторов. Линейная комбинация – это сумма векторов, умноженных на соответствующие числа. Если v1, v2, ..., vn – вектора, a1, a2, ..., an – числа, то их линейная комбинация будет выглядеть так: a1v1 + a2v2 + ... + anvn.
Матричный метод проверки базиса

Сначала необходимо составить матрицу, в которой каждый столбец будет соответствовать одному вектору из рассматриваемого множества. Затем матрица должна быть приведена к ступенчатому виду. Это можно сделать с помощью элементарных преобразований: прибавления к одной строке другой, умножения строки на ненулевое число или перестановки двух строк.
Если в результате приведения матрицы к ступенчатому виду во всех столбцах есть ведущие единицы, а все остальные элементы ниже этих единиц равны нулю, то можно заключить, что исходные векторы являются базисом.
Матричный метод проверки базиса является достаточно простым и эффективным способом определить, являются ли векторы базисом. Он основан на линейной независимости векторов и позволяет быстро и надежно проверить данное свойство.
Скалярное произведение векторов в базисе

Если векторы заданы в базисе, то скалярное произведение можно выразить с помощью матрицы Грама. Матрица Грама составляется из скалярных произведений каждой пары векторов базиса. Для базиса из n векторов матрица Грама будет иметь размерность n×n.
Для вычисления скалярного произведения векторов в базисе необходимо выполнить следующие шаги:
| Шаг 1 | Составить матрицу Грама из скалярных произведений пар векторов базиса. |
| Шаг 2 | Умножить векторы на матрицу Грама. |
| Шаг 3 | Вычислить скалярное произведение полученных векторов. |
Если результат скалярного произведения равен нулю, то векторы ортогональны и могут являться базисом. Если результат скалярного произведения не равен нулю, то векторы не ортогональны и не могут быть базисом.
Скалярное произведение векторов в базисе позволяет определить их ортогональность, что важно при проверке являются ли они базисом.
Линейная комбинация векторов в базисе

Для того чтобы узнать, являются ли векторы базисом, необходимо проверить, можно ли выразить любой вектор данного пространства как линейную комбинацию этих векторов.
Пусть даны векторы v_1, v_2, ..., v_n. Чтобы определить, являются ли они базисом, необходимо проверить два условия:
1. Линейная независимость: векторы не должны быть линейно зависимыми. Это означает, что ни один из векторов не может быть выражен как линейная комбинация других векторов.
2. Генерация пространства: любой вектор данного пространства должен быть выразим через линейную комбинацию заданных векторов. Это означает, что каждый вектор данного пространства можно представить в виде суммы векторов из заданного набора, умноженных на соответствующие коэффициенты.
Если оба этих условия выполняются, то векторы являются базисом данного линейного пространства. Они образуют полную и линейно независимую систему векторов, которая может быть использована для представления любого вектора данного пространства.
Декартова система координат векторов в базисе

Для того чтобы проверить, что векторы являются базисом, необходимо проверить следующие условия:
- Векторы линейно независимы. Это означает, что ни один из векторов не может быть представлен как линейная комбинация других векторов.
- Векторы охвачивают всё пространство. Это означает, что любой вектор в данном пространстве может быть представлен как линейная комбинация базисных векторов.
Если оба условия выполняются, то векторы являются базисом данного пространства. В таком случае, используя декартову систему координат, все векторы можно представить как комбинации базисных векторов с определенными координатами.
Переход между базисами
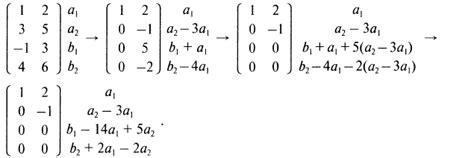
Для выполнения перехода между базисами необходимо знать матрицу перехода, которая отражает способ преобразования координат одних векторов в координаты других векторов. Матрица перехода может быть получена путем применения операции линейного преобразования к векторам нового базиса.
Для перехода от старого базиса к новому необходимо умножить вектор-строку координат старого базиса на матрицу перехода, вычисленную для перехода от нового базиса к старому. Полученная вектор-строка координат в новом базисе является результатом перехода.
В переходе между базисами нередко возникает задача нахождения координат вектора в новом базисе при известных координатах вектора в старом базисе. Эта задача решается путем умножения вектора-столбца координат старого базиса на матрицу перехода, вычисленную для перехода от старого базиса к новому.
Переход между базисами имеет важное значение во многих областях математики и естественных наук, таких как физика, химия, экономика. Например, в физике переход между базисами позволяет производить преобразования координат векторов при переходе в другую систему отсчета.
Практическое применение базисов в векторном анализе

Одно из практических применений базисов - представление векторов в виде линейных комбинаций базисных векторов. Это позволяет нам записывать любой вектор как сумму его компонентов, умноженных на соответствующие базисные векторы. Такое представление упрощает алгебраические вычисления и позволяет более наглядно представить векторы в пространстве.
Одной из практических задач, где базисы находят применение, является решение систем линейных уравнений. Путем представления неизвестных векторов в виде линейных комбинаций базисных векторов, можно перевести систему уравнений на матричную форму и решить ее с использованием методов матричного анализа. Это позволяет нам решать большие и сложные системы уравнений более эффективно и точно.
Базисы также могут быть использованы для представления функций и операторов в векторном анализе. Например, векторные поля могут быть выражены как линейные комбинации базисных векторных полей. Такое представление позволяет нам более удобно анализировать свойства и поведение векторных полей в различных точках пространства.
Кроме того, базисы используются для построения координатной системы в векторном анализе. Базисные векторы выступают в роли осей координатного пространства и позволяют нам определить положение и направление векторов и объектов в пространстве. Это особенно полезно при работе с трехмерными системами или объектами, где векторы определяются в трех направлениях.
| Пример | Практическое применение |
|---|---|
| Представление векторов в виде линейных комбинаций базисных векторов | Упрощение алгебраических вычислений и наглядное представление векторов |
| Решение систем линейных уравнений | Более эффективное и точное решение больших систем уравнений |
| Представление функций и операторов в векторном анализе | Анализ свойств и поведения векторных полей в пространстве |
| Построение координатной системы | Определение положения и направления объектов в пространстве |
Таким образом, базисы играют важную роль в векторном анализе и находят практическое применение во многих задачах. Они позволяют нам более эффективно и точно решать алгебраические и геометрические задачи, а также анализировать свойства и поведение векторов и объектов в пространстве.



