Может ли система неопределенных линейных уравнений быть несовместной и как это влияет на ее решения?

Линейные уравнения – это один из основных элементов алгебры, с которым каждый студент сталкивается в процессе обучения. Однако, не все системы линейных уравнений имеют решения. Некоторые системы могут быть несовместными, что означает отсутствие решений. В этой статье мы рассмотрим особый тип системы линейных уравнений – неопределенные системы и ответим на вопрос: может ли неопределенная система быть несовместной.

Неопределенная система – это система линейных уравнений, в которой количество неизвестных превышает количество уравнений. В такой системе есть бесконечное количество решений, включая все значения неизвестных, которые удовлетворяют уравнениям. То есть, все значения, при которых все уравнения системы выполняются, являются решениями.

Однако, неопределенная система не может быть одновременно несовместной. Несовместная система – это система линейных уравнений, в которой нет ни одного значения, удовлетворяющего всем уравнениям. В несовместной системе, ни одно из уравнений не может быть выполнено для любого значения неизвестных.

Доказательство совместности и несовместности линейных уравнений

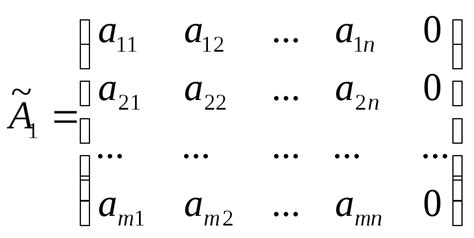
Система линейных уравнений может быть либо совместной, то есть иметь хотя бы одно решение, либо несовместной, когда решений вообще не существует.

Для доказательства совместности или несовместности системы линейных уравнений используются различные методы и алгоритмы.

Для начала, рассмотрим систему линейных уравнений в общем виде:

• a₁₁*x₁ + a₁₂*x₂ + ... + a_1n*x_n = b₁
• a₂₁*x₁ + a₂₂*x₂ + ... + a_2n*x_n = b₂
• ...
• a_m1*x₁ + a_m2*x₂ + ... + a_mn*x_n = b_m

Для проверки совместности системы применяются такие методы:

1. Метод Гаусса: система совместна, если в приведенной матрице коэффициентов нет строчки, состоящей из нулей, а соответствующий столбец свободных членов также не нулевой.
2. Метод Крамера: система совместна, если определитель матрицы коэффициентов не равен нулю.
3. Метод определителей: система совместна, если ранг матрицы коэффициентов равен рангу расширенной матрицы.

Если же система линейных уравнений является несовместной, то решений не существует и эта система называется противоречивой.

Доказательство несовместности системы также может быть осуществлено с помощью различных методов:

• Метод Гаусса: система несовместна, если в приведенной матрице коэффициентов имеется строчка, состоящая из нулей, а соответствующий столбец свободных членов не нулевой.
• Метод Крамера: система несовместна, если определитель матрицы коэффициентов равен нулю, а определитель матрицы уравнений не равен нулю.
• Метод определителей: система несовместна, если ранг матрицы коэффициентов меньше ранга расширенной матрицы.

Важно отметить, что совместность или несовместность системы линейных уравнений может быть использована при решении задач из различных областей математики и физики.

Система совместных линейных уравнений

Система совместных линейных уравнений представляет собой группу линейных уравнений, имеющих одинаковое множество переменных. Она может иметь несколько решений или одно решение, в зависимости от линейной зависимости или независимости уравнений.

Система совместных уравнений называется совместной, если существует хотя бы одно набор значений переменных, который является решением всех уравнений системы. Совместная система может иметь бесконечное множество решений или единственное решение.

Систему совместных уравнений можно решить с помощью метода Гаусса, метода подстановки или метода Крамера. Эти методы позволяют найти значения переменных, удовлетворяющих всем уравнениям системы.

Решение системы совместных уравнений может быть представлено в виде упорядоченного набора значений переменных или в виде графического изображения, позволяющего визуально представить совместное решение.

Система несовместных линейных уравнений

Система линейных уравнений называется несовместной, если не существует решений, которые бы удовлетворяли все уравнения системы одновременно. В таком случае, геометрически это означает, что графики линий, соответствующих уравнениям, не пересекаются в точке или совпадают.

Методы решения несовместных систем линейных уравнений зависят от их размерности. Для маленьких систем можно использовать графический метод: строить графики уравнений и находить точку пересечения. Если такая точка не существует, то система несовместная.

Для более сложных систем удобно применять алгебраические методы. Можно составить расширенную матрицу системы и выполнить элементарные преобразования строк с целью привести ее к удобному для анализа виду. Если в результате получается противоречие, например, 0 = 1, система является несовместной.

Несовместные системы имеют особое значение в теории и практике. Они могут говорить о наличии физического противоречия или ошибки в модели, которую они описывают.

Системы несовместных линейных уравнений встречаются в различных областях науки и техники. Например, в физике несовместные системы могут описывать нереальные физические процессы или неправильно поставленные задачи. В экономике несовместные системы могут говорить о невозможности достижения определенной экономической цели при заданных условиях.

Определение неопределенной системы линейных уравнений

Неопределенная система линейных уравнений представляет собой систему, в которой количество уравнений меньше количества неизвестных переменных. В такой системе уравнений существует бесконечное количество решений, что делает ее несовместной.

Будучи неопределенной, система линейных уравнений не имеет однозначного решения и может иметь множество возможных значений переменных, которые удовлетворяют всем уравнениям системы.

Примером неопределенной системы линейных уравнений может быть:

• 3x + 2y = 10
• 6x + 4y = 20

В данной системе уравнений количество уравнений (2) меньше количества неизвестных (x и y). Более того, оба уравнения являются однотипными и эквивалентными, что делает систему неопределенной.

Такая система может иметь бесконечное количество решений. В данном случае, любая точка на прямой 3x + 2y = 10 будет являться решением системы.

Примеры неопределенной системы линейных уравнений

Условия несовместности неопределенной системы линейных уравнений

1. Коэффициенты перед переменными во всех уравнениях должны быть пропорциональными. Если существует хотя бы одно уравнение, в котором коэффициенты перед переменными не пропорциональны, система будет совместной.
2. Сумма коэффициентов перед переменными в каждом уравнении должна равняться нулю. Если хотя бы в одном уравнении сумма коэффициентов не равна нулю, система будет совместной.
3. Если первые два условия выполнены, проверяем третье условие: сумма коэффициентов перед переменными в каждом уравнении должна быть равной нулю, а все свободные члены должны быть пропорциональными. Если это условие не выполняется, система будет несовместной.

Если хотя бы одно из перечисленных условий не выполняется, неопределенная система линейных уравнений будет несовместной, то есть не будет иметь решений. В противном случае она будет совместной и будет иметь бесконечное количество решений.

Случай, когда сумма свободных членов не равна нулю

Неопределенная система линейных уравнений может быть несовместной, если сумма свободных членов не равна нулю. Это означает, что при подстановке значений переменных, система не сможет найти такие значения, которые бы удовлетворяли всем уравнениям системы одновременно.

Рассмотрим пример. Пусть имеется система линейных уравнений:

3x + 2y = 5

2x - 4y = -7

Если мы попытаемся найти значения переменных x и y, то получим:

3x + 2y = 5 (1)

2x - 4y = -7 (2)

Умножим первое уравнение на 4 и второе уравнение на 3:

12x + 8y = 20 (3)

6x - 12y = -21 (4)

Теперь вычтем уравнение (4) из уравнения (3):

12x + 8y - (6x - 12y) = 20 - (-21)

6x + 20y = 41

Таким образом, получаем уравнение:

6x + 20y = 41

Из этого уравнения ясно, что невозможно подобрать значения переменных x и y таким образом, чтобы оно выполнилось, так как сумма свободных членов отлична от нуля.

Таким образом, в случае, если сумма свободных членов не равна нулю, неопределенная система линейных уравнений будет несовместной. В этом случае решений не существует.

Случай, когда сумма свободных членов равна нулю

В некоторых случаях, система линейных уравнений может быть несовместной, если сумма свободных членов равна нулю. В такой ситуации, уравнения системы не способны обеспечить однозначное решение или привести к согласованным значениям переменных.

Предположим, что имеется система линейных уравнений с n неизвестными и m уравнениями:

a₁₁x₁ + a₁₂x₂ +...+ a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ +...+ a_2nx_n = b₂

...

a_m1x₁ + a_m2x₂ +...+ a_mnx_n = b_m

Если мы заметим, что сумма свободных членов равна нулю, то условия следующие:

b₁ + b₂ +...+ b_m = 0

В этом случае, система линейных уравнений может быть несовместной, так как сумма свободных членов не приводит к ненулевому решению.

Несовместность системы линейных уравнений может быть обнаружена путем анализа матрицы коэффициентов и свободных членов или путем приведения системы к расширенной матрице с последующим применением метода Гаусса.

В данном случае, если сумма свободных членов равна нулю, система линейных уравнений будет иметь бесконечное множество решений или вовсе не будет иметь решений.

Доказательство возможности несовместности неопределенной системы

Неопределенная система линейных уравнений может быть несовместной, то есть может не иметь решений. Для доказательства этого факта рассмотрим следующий пример.

Пусть имеется система линейных уравнений:

a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n = b₂

...

a_m1x₁ + a_m2x₂ + ... + a_mnx_n = b_m

Если количество уравнений (m) больше количества неизвестных (n), то система считается неопределенной.

Для определения возможности несовместности неопределенной системы, составим расширенную матрицу коэффициентов:

[A|B] =

┌─ ─┐

│ a₁₁ a₁₂ ... a_1n │ b₁ │

│ a₂₁ a₂₂ ... a_2n │ b₂ │

│ ... ... ... ... │ ... │

│ a_m1 a_m2 ... a_mn │ b_m │

└─ ─┘

Затем приведем расширенную матрицу к улучшенному ступенчатому виду с помощью элементарных преобразований.

Если в полученной улучшенной ступенчатой матрице обнаружится строка вида [0 ... 0 | c], где c - ненулевое число, то система будет несовместной. В этом случае не существует значений переменных x₁, x₂, ..., x_n, которые удовлетворяют системе уравнений.

Таким образом, доказано, что неопределенная система линейных уравнений может быть несовместной.

Изменение параметров системы

Чтобы определить, может ли неопределенная система линейных уравнений быть несовместной, нужно изменять параметры системы и анализировать полученные результаты.

1. Изменение коэффициентов уравнений:

• Если коэффициенты уравнений изменяются таким образом, что полученные системы имеют одинаковые ранги, то система остается несовместной.
• Если коэффициенты уравнений изменяются таким образом, что ранги полученных систем различаются, то система может стать совместной или остаться несовместной.

2. Изменение свободных коэффициентов:

• Если свободные коэффициенты изменяются таким образом, что полученные системы имеют одинаковые ранги, то система остается несовместной.
• Если свободные коэффициенты изменяются таким образом, что ранги полученных систем различаются, то система может стать совместной или остаться несовместной.

3. Добавление или удаление уравнений:

• Добавление или удаление уравнений может изменить свойства системы и привести к изменению ее совместности.

Изменение параметров системы позволяет установить условия совместности или несовместности неопределенной системы линейных уравнений.