Комплексные числа являются важным понятием в математике и имеют свои особенности. Одним из способов представления комплексных чисел является их представление в тригонометрической форме. Тригонометрическое представление комплексного числа включает в себя длину или модуль числа и его аргумент или угол.
Для определения наличия комплексных чисел в тригонометрической форме необходимо проверить, есть ли у числа мнимая единица i или если его действительная и мнимая часть представлена в виде суммы или произведения синуса и косинуса. Если одно или оба условия выполняются, то это число может быть представлено в тригонометрической форме.
Тригонометрическое представление комплексных чисел используется, например, в решении уравнений и задачах, связанных с колебаниями, а также при изучении и применении фурье-преобразования. При работе с тригонометрической формой комплексных чисел важно уметь переводить их в алгебраическую форму и наоборот.
Определение комплексных чисел
Мнимая единица, обозначаемая символом i, определяется как квадратный корень из отрицательной единицы, то есть i = √(-1). Так как в математике невозможно взять квадратный корень из отрицательного числа, мнимая единица является чисто абстрактным символом.
Комплексное число обычно записывается в виде a + bi, где a - вещественная часть, b - мнимая часть, а символ + обозначает сложение двух частей. Также комплексные числа могут быть представлены в тригонометрической форме, где они записываются как r(cosθ + isinθ), где r - модуль комплексного числа, а θ - его аргумент или угол в полярных координатах.
Комплексные числа широко используются в математике, физике, инженерии и других научных областях. Они играют важную роль в решении различных задач, демонстрируя свою мощь и гибкость в выражении и моделировании разнообразных явлений.
Комплексные числа в тригонометрической форме

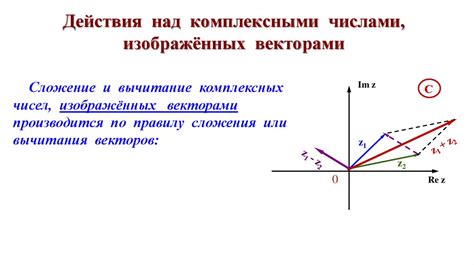
Модуль комплексного числа r определяется как расстояние от начала координат до точки, представляющей комплексное число на комплексной плоскости. Аргумент θ - это угол между положительным направлением оси действительных чисел и радиус-вектором, соединяющим начало координат и точку, представляющую комплексное число.
В тригонометрической форме операции над комплексными числами могут быть выполнены с использованием формул тригонометрии. Например, произведение двух комплексных чисел z1 и z2 можно найти, умножив их модули и сложив аргументы: z = r1r2(cos(θ1 + θ2) + isin(θ1 + θ2)).
Тригонометрическая форма комплексных чисел также связана с экспоненциальной формой записи, где z = re^(iθ), где i - мнимая единица, e - основание натурального логарифма.
Тригонометрическая форма комплексных чисел находит применение в различных областях, таких как электротехника, физика, математика и другие. Она позволяет компактно описывать и оперировать с комплексными числами, что делает их удобными для решения различных задач.
Определение наличия комплексных чисел

Для определения наличия комплексного числа в тригонометрической форме необходимо преобразовать его из алгебраической (декартовой) формы в тригонометрическую форму, где модуль числа представляется расстоянием от начала координат до точки на комплексной плоскости, а аргумент числа определяется как угол между положительным направлением действительной оси и вектором, проведенным из начала координат до точки.
Тригонометрическая форма комплексного числа имеет вид R(cos(α) + i(sin(α))), где R - модуль числа, а α - его аргумент.
Таким образом, если комплексное число имеет ненулевую мнимую часть, то оно является комплексным числом в тригонометрической форме. В противном случае число является действительным и можно записать в алгебраической форме R.
Преобразование числа в тригонометрическую форму
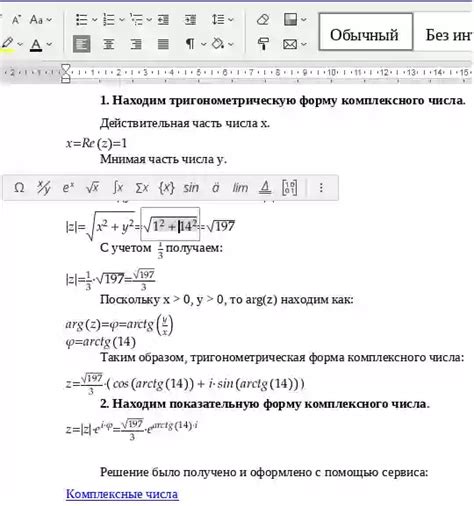
Преобразование числа в тригонометрическую форму позволяет представить его в виде комплексного числа, используя тригонометрические функции синуса и косинуса.
Для преобразования числа в тригонометрическую форму необходимо иметь его мнимую и вещественную части. Мнимая часть числа обозначается как b, а вещественная часть как a. Используя эти значения, можно вычислить модуль числа и его аргумент.
Модуль числа (|z|) вычисляется по формуле:
- |z| = sqrt(a^2 + b^2)
Аргумент числа (arg(z)) вычисляется по формуле:
- arg(z) = atan(b / a), если a > 0
- arg(z) = atan(b / a) + π, если a
- arg(z) = atan(b / a) - π, если a
- arg(z) = π / 2, если a = 0 и b > 0
- arg(z) = -π / 2, если a = 0 и b
- arg(z) = undefined, если a = 0 и b = 0
Итак, мы получили модуль числа и его аргумент. Теперь можем представить число в тригонометрической форме следующим образом:
- z = |z| * (cos(arg(z)) + i * sin(arg(z)))
Где i - мнимая единица, cos - косинус, sin - синус.
Преобразование числа в тригонометрическую форму может быть полезным, особенно при выполнении операций с комплексными числами, такими как умножение, деление и возведение в степень. Это также может упростить визуализацию и анализ данных, представленных в комплексном виде.
Определение наличия комплексных чисел

Тригонометрическая форма записи комплексного числа представляет его в виде z = r(cosθ + isinθ), где r - модуль комплексного числа, θ - аргумент комплексного числа.
Для определения наличия комплексных чисел в тригонометрической форме необходимо проверить, что модуль комплексного числа больше нуля. Если модуль равен нулю, то число является действительным. Если модуль не равен нулю, то число является комплексным.



