Геометрия Лобачевского является одной из альтернативных геометрий, которая возникла в результате исследований русского математика Николая Лобачевского в 19 веке. Основное отличие геометрии Лобачевского от классической евклидовой геометрии заключается в том, что в ней выполняется постулат о параллельности: через одну точку, взятую вне прямой, проходит бесконечно много параллельных прямых.
Пересечение параллельных прямых является одной из ключевых тем в геометрии Лобачевского. В отличие от классической геометрии, где параллельные прямые никогда не пересекаются, в геометрии Лобачевского они могут пересекаться в одной точке или быть сколь угодно далеко от друг друга. Это представляет интересное и необычное свойство, которое находит практическое применение в различных областях, например, в квантовой физике и теории относительности.
Особенностью пересечения параллельных прямых в геометрии Лобачевского является то, что при их пересечении между ними образуется треугольник. Этот треугольник может быть разносторонним, равнобедренным или равносторонним, в зависимости от положения и углового наклона параллельных прямых. Таким образом, геометрия Лобачевского позволяет рассматривать и анализировать геометрические фигуры и объекты, которые не существуют в классической геометрии.
Пересечение параллельных прямых в геометрии Лобачевского
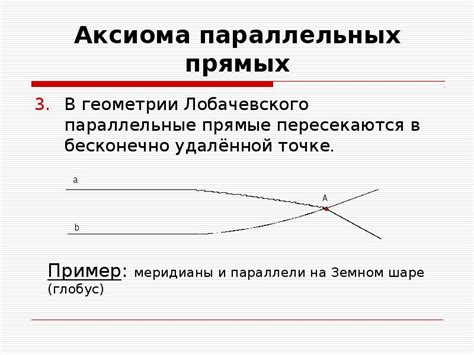
В геометрии Лобачевского существуют два типа параллельных прямых: гиперболические и ультрагиперболические. Гиперболические параллельные прямые стремятся к некоторому предельному положению на границе пространства, которое называется "границей гиперболического пространства". Ультрагиперболические параллельные прямые также стремятся к границе, но приближаются к ней быстрее, чем гиперболические.
При пересечении параллельных прямых в геометрии Лобачевского происходит несколько интересных особенностей. Во-первых, точка пересечения находится на бесконечности, что отличает ее от случая с пересечением параллельных прямых в евклидовой геометрии. Во-вторых, углы между пересекающимися прямыми могут быть как острыми, так и тупыми, в зависимости от их направления и положения на границе пространства. В-третьих, подобно евклидовой геометрии, пересекающиеся прямые образуют пары вертикальных углов, которые равны между собой.
Пересечение параллельных прямых в геометрии Лобачевского имеет большое значение для понимания ее свойств и применения в различных областях. Эта уникальная особенность геометрии Лобачевского позволяет исследовать и моделировать пространство и его свойства с большей гибкостью и точностью.
Определение и основные свойства

В геометрии Лобачевского параллельные прямые определяются как прямые, которые не пересекаются ни в пространстве, ни на бесконечности. Это отличается от евклидовой геометрии, где параллельные прямые никогда не пересекаются. В геометрии Лобачевского, сказанное утверждение не выполняется, и параллельные прямые действительно могут пересекаться.
Одно из ключевых свойств параллельных прямых в геометрии Лобачевского заключается в том, что они имеют равное гиперболическое расстояние между собой. Гиперболическое расстояние - это мера расстояния в геометрии Лобачевского и отличается от евклидового расстояния.
Еще одним важным свойством параллельных прямых в геометрии Лобачевского является то, что они могут быть сколь угодно близко друг к другу. В евклидовой геометрии, параллельные прямые будут иметь постоянное расстояние между собой. В геометрии Лобачевского, параллельные прямые могут быть настолько близко друг к другу, что между ними будет ненулевая площадь.
В контексте геометрии Лобачевского, пересечение параллельных прямых является важным свойством, которое имеет множество интересных математических и геометрических последствий. Изучение этих свойств и особенностей помогает лучше понять и визуализировать пространство в рамках геометрии Лобачевского.
Построение пересечения
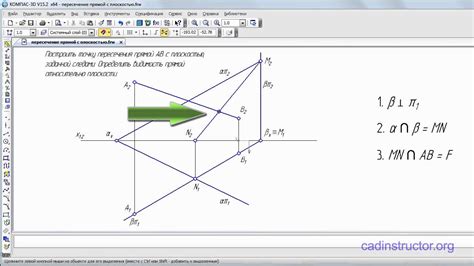
Для построения пересечения параллельных прямых в геометрии Лобачевского необходимо выполнить следующие шаги:
- Выберите две параллельные прямые, например, AB и CD, и выберите произвольную точку на одной из них, например, точку E на прямой AB.
- Из точки E проведите перпендикуляр к прямой CD, например, отрезок EF.
- С второй прямой CD проведите перпендикуляр, параллельный отрезку EF, например, отрезок GH.
- Точка пересечения отрезков EF и GH будет искомой точкой пересечения прямых AB и CD.
Этот метод позволяет найти точку пересечения параллельных прямых в геометрии Лобачевского без использования угловых построений и аксиом Евклида о параллельных прямых. В геометрии Лобачевского пересечение параллельных прямых может иметь место и находиться в пределах плоскости, что отличает ее от геометрии Евклида.
Взаимное расположение прямых на плоскости
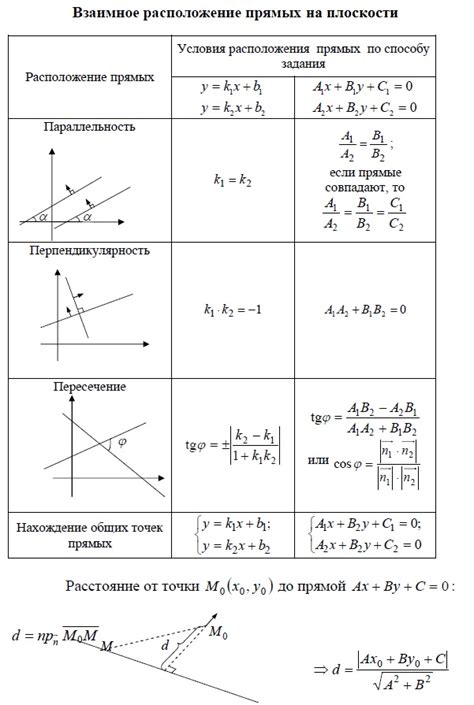
В геометрии Лобачевского взаимное расположение прямых на плоскости имеет свои особенности и отличия от евклидовой геометрии.
Пересечение двух параллельных прямых происходит в геометрии Лобачевского, и это является основной отличительной особенностью данной геометрии от евклидовой геометрии. В евклидовой геометрии параллельные прямые никогда не пересекаются, однако в геометрии Лобачевского они пересекаются в точке бесконечности.
Такое пересечение прямых на плоскости геометрии Лобачевского может быть представлено следующим образом:
Если взять две параллельные прямые, то они будут иметь одно общее свойство – их расстояние будет постоянным и растягиваться в бесконечность. При этом, при удалении от центра плоскости, прямые будут все более и более сближаться, пока в итоге не пересекутся в точке бесконечности.
Точка бесконечности в геометрии Лобачевского представляет собой идеализированную точку, которая находится на бесконечном удалении от обычных точек плоскости. Она является точкой пересечения всех параллельных прямых.
Таким образом, в геометрии Лобачевского не существует параллельных прямых, которые не пересекаются, в отличие от евклидовой геометрии. Взаимное расположение прямых на плоскости Лобачевского обладает своими особенностями и позволяет исследовать геометрические объекты, которые в евклидовой геометрии не существуют.
Расширенная геометрия Лобачевского
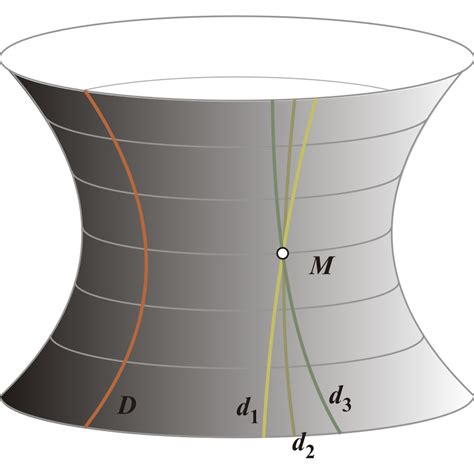
В расширенной геометрии Лобачевского добавляется понятие "точки в бесконечности", которые представляют собой точки на бесконечности прямой. Таким образом, на обычных прямых Лобачевского есть две точки в бесконечности - одна на "плюс-бесконечности" и одна на "минус-бесконечности". Параллельные прямые пересекаются в точке в бесконечности, а любая прямая пересекает сколько угодно параллельных прямых на "бесконечности".
Одно из основных применений расширенной геометрии Лобачевского - строительство моделей гиперболической геометрии. С помощью расширенной геометрии Лобачевского можно рассматривать модель полной плоскости Лобачевского, где прямые и точки находятся в соответствии с правилами геометрии Лобачевского. Это позволяет исследовать свойства и особенности гиперболической геометрии, которая имеет много применений в математике и физике.
| Свойства расширенной геометрии Лобачевского: |
|---|
| 1. В расширенной геометрии Лобачевского любая прямая пересекает сколько угодно параллельных прямых. |
| 2. Параллельные прямые пересекаются в точке в бесконечности. |
| 3. Сумма углов треугольника в расширенной геометрии Лобачевского всегда меньше 180 градусов. |
| 4. Расстояние между двумя точками в расширенной геометрии Лобачевского может быть бесконечным. |
Применение в реальной жизни

Геометрия Лобачевского и пересечение параллельных прямых имеют широкое применение как в теории, так и в практике. Ниже приведены некоторые области, где эти концепции находят свое применение:
- Навигация и картография: Геометрия Лобачевского используется для построения карт и навигационных систем, особенно в местах с большими масштабами. Она помогает определить кратчайший путь между двумя точками на поверхности Земли и учитывает изгибы и кривизну.
- Транспорт и инфраструктура: При проектировании дорог, мостов и железных дорог геометрия Лобачевского применяется для оптимизации путей и минимизации времени и дистанции.
- Космические исследования: При планировании космических миссий и траекторий космических объектов геометрия Лобачевского позволяет учесть кривизну пространства и выбрать оптимальные маршруты.
- Телекоммуникации: При проектировании сетей связи и передачи данных геометрия Лобачевского используется для оптимизации сигнальных маршрутов и повышения эффективности передачи информации.
- Астрономия: В астрономии геометрия Лобачевского применяется при изучении кривизны пространства и времени, а также при моделировании движения небесных тел.
- Искусство и дизайн: Геометрия Лобачевского может быть использована в дизайне архитектуры, мебели и графики для создания необычных и впечатляющих форм и композиций.
Все эти примеры демонстрируют, что геометрия Лобачевского не только имеет теоретическую ценность, но и находит практическое применение в различных областях нашей жизни.



