Задача поиска такого значения х, при котором функция равна нулю, является одной из основных задач математического анализа. Эта проблема возникает во многих областях науки и техники, включая физику, экономику и компьютерные науки.
Чтобы найти такое значение х, необходимо рассмотреть уравнение функции и использовать методы решения уравнений. Существуют различные методы для решения уравнений, включая методы аналитического и численного решения.
Методы аналитического решения уравнений основаны на применении математических операций и свойств для получения точного значения х. Однако не всегда возможно найти аналитическое решение, особенно для сложных функций.
В таких случаях применяются методы численного решения, которые основаны на аппроксимации значения х с определенной точностью. Такие методы включают в себя итерационные и интерполяционные методы, методы половинного деления и методы Ньютона-Рафсона.
Существует ли решение?
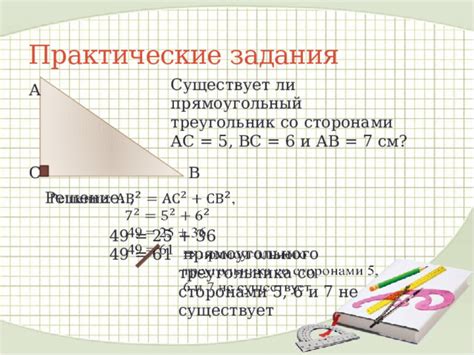
Для определения существования решения необходимо рассмотреть заданную функцию и выяснить, существуют ли такие значения переменных, при которых она равна нулю.
В случае, если функция задана аналитически, то для нахождения решения можно использовать методы алгебры и анализа. Например, можно решить уравнение, полученное путем приравнивания функции к нулю и найти значения переменных, при которых оно выполняется.
Если функция задана графически, то для определения существования решения можно визуально проанализировать график функции. Если на графике есть точки пересечения с осью абсцисс, то существуют значения переменных, при которых функция равна нулю.
В некоторых случаях решение может быть найдено численными методами, например, методом бисекции или методом Ньютона. Эти методы позволяют приближенно находить значения переменных, при которых функция равна нулю.
В общем случае, для определения существования решения необходимо тщательно анализировать заданную функцию и применять соответствующие методы для нахождения решения.
Анализ функции

Для анализа функции на наличие такого значения х, при котором функция равна нулю, необходимо провести ряд операций и исследований. Этот процесс обычно называется "решением уравнения" или "нахождением корней функции".
Итак, начнем с анализа функции в общем виде. Для начала, определим, что такое "функция равна нулю". Если мы говорим о функции f(x), то это означает, что f(x) = 0. Цель анализа функции состоит в том, чтобы найти значения х, при которых f(x) равна нулю.
Существует несколько методов для анализа функций и поиска таких значений х. Один из самых распространенных методов - это графический метод. Для этого мы строим график функции и ищем точки пересечения его с осью x (ось абсцисс).
Другой метод - это алгебраический метод. Для этого мы используем различные алгебраические приемы для решения уравнения f(x) = 0. Например, мы можем факторизовать функцию и найти корни уравнения путем решения множителей.
Кроме того, мы можем использовать численные методы, такие как метод половинного деления или метод Ньютона, чтобы приближенно найти значения х, при которых функция равна нулю.
Однако следует отметить, что не всегда существует такое значение х, при котором функция равна нулю. В этом случае мы можем говорить о том, что функция не имеет корней или о том, что решение не существует в рамках выбранной системы чисел. Например, функция f(x) = x^2 + 1 не имеет корней в действительных числах, но имеет комплексные корни.
В итоге, анализ функции на наличие такого значения х, при котором функция равна нулю, является важным шагом при решении различного рода задач и проблем в математике и науке.
Методы решения уравнений

Существует несколько методов для решения уравнений. Один из самых простых методов - это метод подстановки. Он заключается в последовательном определении значения переменной и проверке равенства уравнения нулю. Если равенство выполняется, то найдено искомое значение переменной.
Другим методом является метод графического представления. При этом строится график функции и определяется точка пересечения графика с осью абсцисс. Если координата этой точки равна искомому значению переменной, то уравнение выполняется.
Более сложные уравнения могут решаться с использованием алгебраических методов, таких как метод подбора, метод Крамера, метод Гаусса и метод Ньютона. Каждый из этих методов имеет свои особенности и применяется в зависимости от конкретной ситуации.
Один из наиболее эффективных и точных методов решения уравнений - метод численных итераций. Он основан на последовательном приближении к искомому значению переменной путем выполнения итераций. Этот метод позволяет найти решение с любой заданной точностью.
В зависимости от типа уравнения и его сложности, выбираются соответствующие методы решения. Важно учитывать особенности каждого метода и применять их с учётом контекста задачи. Все эти методы дают возможность найти значения переменной, при которых уравнение становится нулевым.
Графический способ
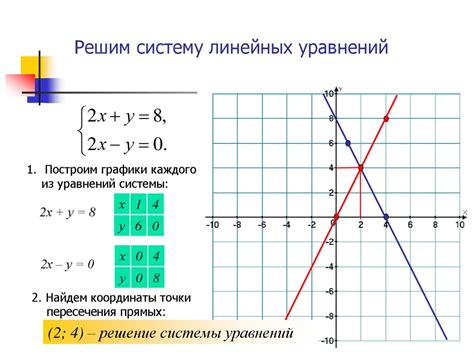
Графический способ решения уравнений и поиска значений, при которых функция равна нулю, основывается на анализе графика функции.
- Постройте график функции на координатной плоскости.
- Проанализируйте график и определите, есть ли точки, в которых функция пересекает ось OX (горизонтальная ось) или значение функции равно нулю.
- Если такие точки существуют, то значит есть значения x, при которых функция равна нулю. Запишите эти значения x.
Преимущество графического способа заключается в его интуитивности и наглядности. Однако он имеет некоторые ограничения, так как не всегда возможно точно определить значения x, при которых функция равна нулю только по графику. Также стоит помнить, что графический способ не является формальным математическим доказательством, а скорее методом предположения и проверки.
Алгебраическое решение

Для нахождения такого значения х, при котором функция равна нулю, необходимо решить алгебраическое уравнение, полученное путем приравнивания функции к нулю.
1. Изначально записываем функцию в виде уравнения: f(x) = 0
2. Решаем уравнение, используя алгебраические методы и техники. Это могут быть, например, методы факторизации, полного квадрата, графического анализа или методы численного решения, такие как метод Ньютона.
3. Найденные значения х, при которых функция равна нулю, являются решениями исходной задачи.
Примечание: В некоторых случаях, функция может не иметь решений или иметь бесконечное количество решений. В таких случаях, алгебраическое решение может не существовать или быть неконкретным.
Рациональные корни
Рациональные числа – это числа, которые могут быть представлены в виде дробей, где числитель и знаменатель являются целыми числами. Например, 1/2, 3/4 и -2/5 являются рациональными числами, так как они могут быть представлены в виде дробей.
Для того чтобы найти рациональные корни функции, можно использовать метод подстановки. Допустим, имеется функция f(x) = x^2 - 4x + 3. Чтобы найти рациональные корни этой функции, можно подставить различные значения рациональных чисел вместо переменной x и проверить, при каком значении функция равна нулю.
Например, если подставить x = 1, то получим f(1) = 1^2 - 4*1 + 3 = 0. Это означает, что x = 1 является рациональным корнем функции f(x).
Если функция имеет рациональные корни, то они могут быть найдены путем решения уравнения на равенство нулю. Решить такое уравнение можно методами алгебры, используя факторизацию, полиномиальные и квадратичные формулы.
Рациональные корни могут быть полезными при анализе и построении графиков функций, а также для решения различных математических проблем и задач в различных областях науки и техники.
Комплексные корни
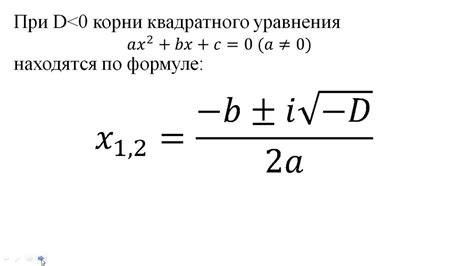
При решении уравнений и задач, связанных с нахождением нулей функций, возможно появление комплексных корней. Комплексный корень представляет собой число, состоящее из действительной и мнимой части.
Если рассматриваемая функция имеет комплексные коэффициенты или содержит иррациональные выражения, то ее корни могут быть комплексными числами.
Комплексные корни функции могут иметь вид a + bi, где a и b - действительные числа, а i - мнимая единица (i^2 = -1).
Существуют специальные формулы для вычисления комплексных корней функций, такие как формула Муавра и метод графического построения комплексных чисел.
Комплексные корни могут иметь различную геометрическую интерпретацию. Они могут соответствовать точкам на комплексной плоскости или служить значениями параметров для определенных фигур.
Определение наличия комплексных корней может быть важным в задачах, связанных с исследованием функций и построением их графиков.
Пример:
Рассмотрим квадратное уравнение:
x^2 + 4x + 5 = 0
Дискриминант этого уравнения равен: D = 4 - 4 * 1 * 5 = -4.
Поскольку дискриминант отрицательный, уравнение имеет комплексные корни.
Решим уравнение, используя формулу для комплексных корней:
x = (-b ± √D) / (2a)
x = (-4 ± √(-4)) / (2 * 1)
x = (-4 ± 2i) / 2
x = -2 ± i
Таким образом, уравнение имеет два комплексных корня: x1 = -2 + i и x2 = -2 - i.
Проверка решений
Для проверки решения уравнения, необходимо подставить найденное значение переменной в уравнение и выполнить соответствующие вычисления. Если после этих вычислений получается ноль, то найденное значение является корнем уравнения. Если же результат не равен нулю, то найденное значение не является корнем уравнения и требуется продолжить поиск других возможных решений.
При проверке решения неравенства, необходимо подставить найденное значение переменной в неравенство и выполнить соответствующие вычисления. Затем нужно анализировать полученный результат с учетом знака неравенства. Если неравенство выполняется, то найденное значение является решением неравенства. Если же неравенство не выполняется, то найденное значение не является решением неравенства и требуется продолжить поиск других возможных решений.
Таким образом, проверка решений играет важную роль в математике, позволяя убедиться в правильности найденных значений и определить, являются ли они решениями уравнений и неравенств.



