Векторы в ОГЭ

Векторы – одна из основных тем в школьной программе по математике. Понимание основных понятий векторов и умение решать задачи с их использованием является неотъемлемой частью подготовки к ОГЭ. В данной статье мы рассмотрим основные темы, которые встречаются в заданиях по векторам на ОГЭ, и приведем примеры задач для закрепления материала.

Одним из основных понятий векторов является направление. Векторы могут быть направлены вверх, вниз, вправо, влево или под различными углами. Например, ветер может дуть с севера на юг, а автомобиль может двигаться с востока на запад. Также векторы характеризуются своей длиной, которая может быть равна 0 (нулевой вектор) или положительному числу (ненулевой вектор).

В задачах на ОГЭ по векторам часто требуется найти сумму или разность векторов, а также определить координаты конечной точки, если известны координаты начальной точки и вектор перемещения. Помимо этого, векторы используются для решения задач на пропорциональность, подобие и равенство треугольников.

Понимание основных тем векторов и умение решать задачи с их использованием поможет ученикам успешно справиться с заданиями по математике на ОГЭ. Для закрепления материала рекомендуется решать множество различных задач по векторам и самостоятельно придумывать новые подходы к их решению.

Основные темы по векторам в заданиях ОГЭ:

1. Определение вектора и его основные свойства.

2. Операции с векторами: сложение, вычитание, умножение на число.

3. Координаты вектора в прямоугольной системе координат.

4. Равенство векторов.

5. Геометрический смысл операций над векторами.

6. Прямоугольные и неравнобедренные треугольники.

7. Параллельные и перпендикулярные векторы.

8. Нахождение длины вектора (модуля), его проекций на оси координат.

9. Геометрическое место точек (прямых, плоскостей) в пространстве.

10. Понятие коллинеарных и компланарных векторов.

Владение этой темой поможет вам успешно решать задачи по векторам на ОГЭ.

Основные темы и примеры задач

Определение вектора и его характеристики:

Вектор - это пространственная величина, которая характеризуется направлением и длиной. Направление задается с помощью угла между вектором и выбранной осью координат, а длина - с помощью модуля (абсолютной величины) вектора.

Пример задачи: Найдите модуль вектора AB, если его координаты равны A(3, 4) и B(-1, 2).

Операции над векторами:

К операциям над векторами относятся: сложение, вычитание, умножение на число и скалярное (скалярное) произведение.

Пример задачи: Даны векторы a и b с координатами a(2, -3) и b(5, 2). Найдите вектор c, который равен разности векторов a и b.

Геометрические свойства векторов:

Векторы обладают рядом геометрических свойств: коллинеарность, компланарность, ортогональность и параллельность.

Пример задачи: Пусть вектора a и b образуют угол 60 градусов. Найдите скалярное произведение векторов, если их длины равны 3 и 4 соответственно.

Решение геометрических задач с использованием векторов:

Векторы могут быть использованы для решения различных геометрических задач, таких как нахождение площадей треугольников, проверка належности точек прямым или плоскостям и определение типа треугольника.

Пример задачи: Даны координаты вершин треугольника: A(1, 2), B(4, 1) и C(3, 4). Определите тип треугольника (равносторонний, равнобедренный или разносторонний).

Определение вектора

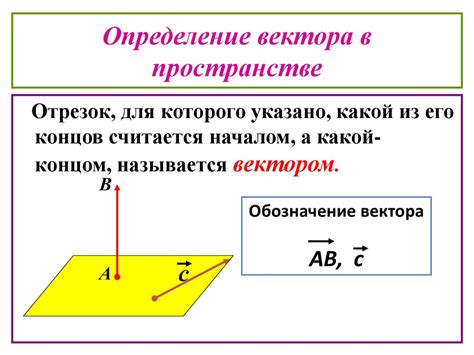
Вектор обычно обозначается латинской буквой с надстрочной стрелкой, например, AB или a. Вектор может быть задан координатами его начала и конца или с помощью его модуля и направления. Координаты вектора могут быть представлены как упорядоченные пары чисел или как компоненты вектора в пространстве. Векторы также могут быть сложены, вычитаны, умножены на скаляр и иметь другие операции.

Основные свойства вектора включают:

1. Длина (модуль)	Определяется математической величиной вектора и обозначается \|AB\| или a.
2. Направление	Задается углом, под которым вектор направлен относительно некоторой системы координат.
3. Точка приложения (начало)	Задает место, где вектор начинается.

Примеры задач, связанных с векторами, могут включать векторное сложение, вычитание векторов, определение компонент вектора, нахождение модуля и направления вектора, решение геометрических задач, анализ движения и многое другое. Понимание основных понятий и свойств векторов позволяет решать разнообразные задачи и применять векторный подход в решении различных задач и задач на ОГЭ.

Сложение и вычитание векторов

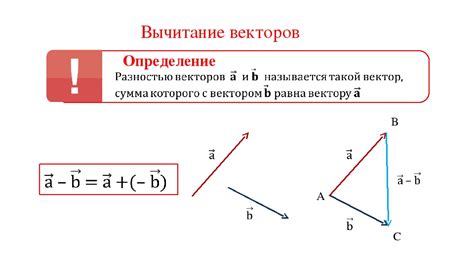
Для сложения векторов необходимо добавить соответствующие компоненты векторов по отдельности. Например, если у нас есть векторы A(2, 3) и B(1, -1), то сумма векторов A и B будет вектором C(3, 2). Аналогично, для вычитания векторов, необходимо вычесть соответствующие компоненты векторов.

Векторы можно выразить в виде отрезков на координатной плоскости. Вектор с началом в точке (0, 0) и концом в точке (2, 3) будет соответствовать отрезку на координатной плоскости. При сложении векторов A и B, мы перемещаем конец вектора A к концу вектора B, таким образом, получаем вектор C.

Сложение и вычитание векторов можно представить графически с помощью параллелограмма или метода параллелограмма. При сложении двух векторов, мы строим параллелограмм с одним вектором в качестве диагонали и используем второй вектор, чтобы получить диагональ параллелограмма. Вектор, соединяющий начало и конец этой диагонали, будет результирующим вектором.

Также, можно выразить сложение и вычитание векторов с помощью скалярных произведений. Используя скалярные произведения, мы можем определить угол между векторами и длину результирующего вектора. Формулы для вычисления скалярного произведения и модуля вектора помогут нам провести эти вычисления.

Умножение вектора на число

Вектор может быть умножен на число (скаляр), при этом каждая компонента вектора умножается на это число.

Для умножения вектора на число, нужно умножить каждую компоненту вектора на это число.

Пусть имеется вектор \(\overrightarrow{AB} = (a, b)\) и число \(k\). Умножение вектора на число записывается как \(k\cdot\overrightarrow{AB}\).

Результатом умножения вектора на число является новый вектор, у которого каждая компонента умножена на число:

Исходный вектор	Число	Результат
\(\overrightarrow{AB} = (a, b)\)	\(k\)	\(k\cdot\overrightarrow{AB} = (k\cdot a, k\cdot b)\)

Умножение вектора на число имеет ряд свойств:

Если число равно 0, то результатом умножения будет нулевой вектор.
Если число положительное, то умножение увеличивает длину вектора в число раз и не меняет его направление.
Если число отрицательное, то умножение меняет направление вектора на противоположное и не меняет его длины.

Умножение вектора на число широко применяется в физике, геометрии и других областях математики для изменения масштаба и направления векторов.

Компоненты вектора

Компоненты вектора могут быть положительными или отрицательными, в зависимости от направления проекции. Они обычно обозначаются буквами с верхним индексом, указывающим на соответствующую ось: х - горизонтальная ось, у - вертикальная ось, z - ось глубины.

Для удобства работы с векторами можно использовать специальные математические операции и формулы для определения компонентов.

В случае двумерной системы координат, вектор может быть представлен как сумма двух компонентов: горизонтальной и вертикальной.
Компоненты вектора можно вычислить, зная его длину и угол, который он образует с положительным направлением оси координат.
Для вычисления компонентов вектора могут быть использованы тригонометрические функции, такие как синус и косинус.

Знание компонентов вектора позволяет удобно производить все необходимые операции с векторами, такие как сложение, вычитание, умножение на число и т.д.

Ортогональность векторов

Векторы называются ортогональными, если угол между ними равен 90 градусам. Ортогональные векторы обладают значимыми свойствами и широко применяются в различных областях, включая геометрию, физику и информатику.

Сложение и вычитание ортогональных векторов дают новый вектор, который также будет ортогонален исходным векторам. Это свойство соответствует геометрическому представлению ортогональности, так как сумма или разность ортогональных векторов дает прямоугольный треугольник.

Ортогональные векторы также полезны при решении задач на проекции векторов. При проецировании вектора на другой вектор, ортогональная составляющая нулевая, что позволяет упростить вычисления. Также ортогональные векторы используются при решении систем линейных уравнений и построении ортогональных базисов.

Ортогональность векторов может быть проверена с помощью их скалярного произведения. Для двух векторов a и b их скалярное произведение равно 0, если векторы ортогональны: a · b = 0.

Знание свойств и применение ортогональных векторов позволяет более эффективно решать задачи векторной алгебры и применять их в практических ситуациях. Поэтому понимание ортогональности векторов является важным элементом подготовки к ОГЭ по математике.

Проекция вектора

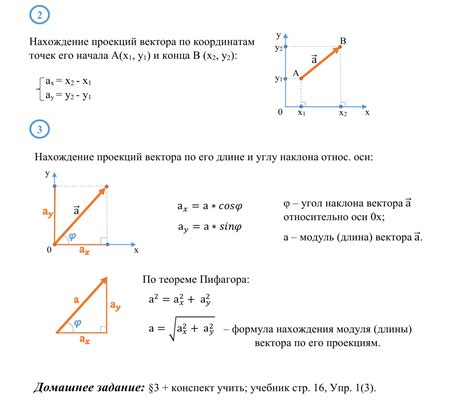
Проекция вектора на ось координат - это скалярное значение, которое показывает, насколько вектор сонаправлен или противонаправлен соответствующей оси. Проекция вектора на ось координат можно найти с помощью формулы:

Для вектора a = (a₁, a₂) проекция на ось OX равна a₁
Для вектора a = (a₁, a₂) проекция на ось OY равна a₂

Проекция вектора на другой вектор - это вектор, который получается проекцией изначального вектора на другой, заданный вектор. Проекция вектора a на вектор b обозначается proj_ba и может быть найдена с помощью формулы:

proj_ba = (a · b/|b|²) * b, где · - скалярное произведение, |b| - длина вектора b.

Проекция вектора позволяет определить, насколько вектор сонаправлен с осью или с другим вектором, что часто является полезной информацией при решении задач по векторам.

Задачи на векторы в ОГЭ

Задача 1

Даны два равных по длине отрезка AB и CD, такие что AB = CD = 5. Найдите вектор AD.

Решение:

Так как отрезки AB и CD равны, то векторы AB и CD тоже равны. Поэтому вектор AD можно найти как разность векторов AB и CD: AD = AB - CD.

Так как длина отрезка AB равна 5, вектор AB имеет координаты (5, 0) в координатной плоскости. Так как CD равно по длине и направлению AB, вектор CD тоже имеет координаты (5, 0).

Таким образом, вектор AD равен разности (5, 0) - (5, 0) = (0, 0).

Ответ: вектор AD равен (0, 0).

Задача 2

На координатной плоскости даны точки A(1, 2), B(4, 3) и C(5, 5). Найдите длину вектора AB и координаты вектора AC.

Решение:

Длину вектора AB можно найти с помощью формулы: √((x2 - x1)^2 + (y2 - y1)^2).

Для данной задачи: x1 = 1, y1 = 2, x2 = 4, y2 = 3.

Тогда длина вектора AB равна √((4 - 1)^2 + (3 - 2)^2) = √(9 + 1) = √10.

Координаты вектора AC можно найти как разность координат точек A и C: AC = C - A.

Для данной задачи: координаты точки A (1, 2), координаты точки C (5, 5).

Тогда координаты вектора AC равны (5 - 1, 5 - 2) = (4, 3).

Ответ: длина вектора AB равна √10, координаты вектора AC равны (4, 3).

Задача 3

На координатной плоскости даны точки A(1, -3), B(2, 4) и C(-6, 0). Найдите векторы AB и AC, и найдите угол между ними.

Решение:

Вектор AB можно найти как разность координат точек A и B: AB = B - A.

Для данной задачи: координаты точки A (1, -3), координаты точки B (2, 4).

Тогда вектор AB равен (2 - 1, 4 - (-3)) = (1, 7).

Вектор AC можно найти как разность координат точек A и C: AC = C - A.

Для данной задачи: координаты точки A (1, -3), координаты точки C (-6, 0).

Тогда вектор AC равен (-6 - 1, 0 - (-3)) = (-7, 3).

Угол между векторами AB и AC можно найти с помощью формулы: cos(θ) = (AB*AC) / (|AB|*|AC|), где AB*AC - скалярное произведение векторов AB и AC, |AB| и |AC| - длины векторов AB и AC.

Для данной задачи: AB*AC = (1*1) + (7*3) = 1 + 21 = 22, |AB| = √(1^2 + 7^2) = √50, |AC| = √((-7)^2 + 3^2) = √58.

Тогда cos(θ) = 22 / (√50 * √58) ≈ 0.942.

Угол θ ≈ arccos(0.942) ≈ 20.997°.

Ответ: вектор AB равен (1, 7), вектор AC равен (-7, 3), угол между ними примерно 20.997°.

Векторы в ОГЭ — основные темы и примеры задач для успешной подготовки